Why there is so many constants in equations?

I will tell you the secret of constants in mathematical equations. They are not intruded or the error or nothing, but it is essential part of the equation. I will tell you some facts while going on your story. I will exemplify what you want in this story.
Consider you are a young scientist. You close your room's door and start experimenting on something when you get leisure time on Sundays. You are doing something seriously on your table, with an electrical circuit. Your aim is to find the dependence of a node voltage X (ie, a voltage in a part of the circuit). You came to know that X depend upon the supply voltage V. You start experimenting and plot graph of X for different values of V. Then you
got a graph like this:
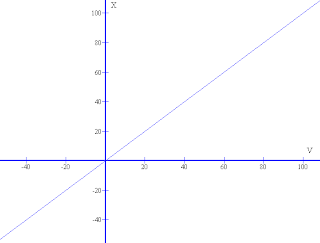
It is perfectly linear. So you write,
X is directly proportional to V
To be more specific, X increases for an equivalent increase in V. You repeated your experiment and plot another characteristics with time. This time, your supply voltage kept constant. Plot X with time t.

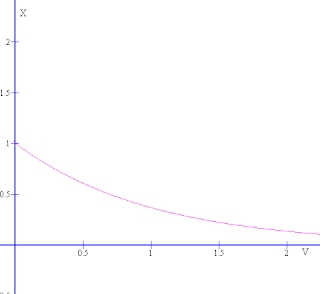From the plot, it easy to find that dependence is,

X is directly proportional to e^(-t)

Then from the above town experiments, you can write that,

X is directly proportional to V*e^(-t)
ie, X = K*V*e^(-t) where a K is the proportionality constant.

You can find K from single experiment. Once you got the value X when for a particular V and t,

K = X/(V*e^(-t)

But I want to tell you that your experiment as well as your mathematical expression is not perfectly true. A true dependence of X on it's environment will be very complex and tedious to express in mathematical form. Your X may depend on the atmospheric pressure, temperature, material properties,...raining in New Delhi,.....war on Iraq and so so.
After several years, you repeated your experiment and find that X depending on temperature also. Temperature has a direct linear relationship (like V) on X. But last time, you didn't got it. What's the reason? You were not aware of that, you did the experiment in room temperature itself. But this time you get different answers in day and chilled night. Now you modify your equation as,

X is directly proportional to V*T*e^(-t) where T is the temperature
X = L*V*T*e^(-t) where L is the proportionality constant.

Here I want a point to stress. Do you think your previous equation was wrong? Not at all. It is correct in an isothermal environment. But it become wrong in a temperature varying environment. A single measurement depending upon many things in the surroundings. But many of them can be ignored, because, they have less relationship with X. Something can't be ignored, but they may not be measurable (such as number of electron collision per second).In such cases, just put a constant for that, as long as they are constants. To be more clear, if your experiment depends upon the radius of earth, just put it as a constant in your equation. But when you do the experiment in moon, your experiment may troubled, unless you replaced the radius of earth with moon. I meant that variables can be considered as a constant or variable according to the environment.